Aufgaben zu Buchstabengruppen lösen – Übungen mit Lösungen

Aufgaben zu Buchstabengruppen kennen die wenigsten Schüler aus der Schule. Buchstabengruppen begegnen uns häufig im Assessment Center, im Einstellungstest, oder anderen Auswahlverfahren das erste mal im Leben. Ein Grund mehr sich gezielt auf diesen Aufgabentyp zum logischen Denken vorzubereiten.

Was sind Buchstabengruppen?

Bei einer Buchstabengruppe handelt es sich um mehrere Buchstaben aus dem Alphabet, welche nach bestimmten Regeln zusammengesetzt wurden. Durch logisches Denken, Grundkenntnissen aus der Mathematik und dem Beherrschen des Alphabets gilt es in Auswahlverfahren die Regeln zu bestimmten Buchstabengruppen ausfindig zu machen.

Welche Aufgaben gibt es zu Buchstabengruppen?

Bei Aufgaben zu Buchstabengruppen unterscheiden wir nach

• Buchstabengruppen fortsetzen und
• Abweichungen in Buchstabengruppen finden.

Weiter unten finden sich einige Beispiele zu beiden Aufgabentypen. Neben Buchstabengruppen gibt es auch Aufgaben zu Buchstabenreihen und Buchstabensalat, welche gerne im Assessment Center eingesetzt werden.

Wie kann man Buchstabengruppen entschlüsseln?

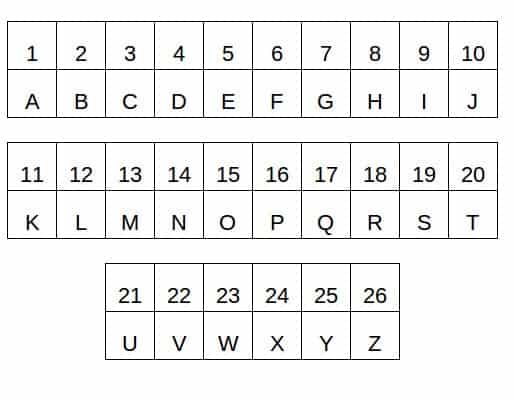
Um die passende Regel zu einer Buchstabengruppe zu finden, sollte man ein Alphabet mit Nummern zur Hand nehmen. Falls keines zur Hand, schreiben Sie sich einfach alle Buchstaben hintereinander auf und neben jedem Buchstaben aufsteigend die zugehörige Stelle im Alphabet, beispielsweise so:

1. A/a
2. B/b
3. C/c
4. D/d
5. E/e
6. F/f
7. G/g
8. H/h
9. I/i
10. J/j
11. K/k
12. L/l
13. M/m
14. N/n
15. O/o
16. P/p
17. Q/q
18. R/r
19. S/s
20. T/t
21. U/u
22. V/v
23. W/w
24. X/x
25. Y/y
26. Z/z

Beispielaufgabe 1
Welche Buchstabengruppe ist nicht nach der gleichen Rechenregel wie die anderen zusammengesetzt?
a         b         c         d
YXVW ONPM TSQR DCAB
Schitt 1: Schreiben Sie die Buchstabengruppen als Zahlengruppen anhand der Alphabettabelle auf:
a                    b                    c                    d
25,24,22,23   12,14,16,13   20,19,17,18  4,3,1,2
Schritt 2: Setzen Sie die Zahlen in jeder Gruppe ins Verhältnis. Verwenden Sie dabei die Grundrechenarten und Ermitteln Sie die Differenz, Summe, etc. Im Beispiel 1 subtrahieren wir immer die aktuelle Zahl von der jeweils nächsten Zahl.
a                b              c               d
-1, -2, +1   +2,+2,-3   -1, -2,+1   -1, -2, +1
Schritt 3: Finden Sie die Gruppe mit einer abweichenende Differenz im Vergleich zu den anderen. In diesem Beispiel ist es die Gruppe B, welche eine abweichende Differenz aufweist, somit lautet die Lösung B.

Wie lassen sich Buchstabengruppen fortsetzen?

Ähnlich wie bei “Abweichungen in Buchstabengruppen” muss beim “Buchstabengruppen fortsetzen” eine Rechenregel gefunden werden. Erschwerend kommt allerdings hinzu, dass es zwischen den Buchstabengruppen häufig eine weitere Rechenregel gibt.
Beispielaufgabe 2
Setzen Sie die folgenden Buchstabengruppen fort:
a           b          c           d
ACEG   JLNP   SUWY   ?
Schritt 1:
1,3,5,7   10,12,14,16  19,21,23,25
Schritt 2:
+2,+2,+2  +2,+2,+2  +2,+2,+2
Schritt 3: (Zweite Rechenregel zwischen den Buchstabengruppen)
+2,+2,+2  +3,+2,+2,+2  +3,+2,+2,+2
Schritt 4: (Zahlengruppen nach der gleichen Regel fortsetzen)
1,3,5,7   10,12,14,16  19,21,23,25   28,30,32,34
Da es nur 26 Grundbuchstaben (ohne Umlaute und ß) gibt, werden alle Zahlen über 26 nochmals durch 26 subtrahiert:
1,3,5,7   10,12,14,16  19,21,23,25   2,4,6,8
Schritt 5: (Zahlengruppen in Buchstabengruppen umwandeln)
a           b          c            d
ACEG   JLNP   SUWY   BDFH