Was ist ein Flaschenzug?
Ein Flaschenzug ist eine Vorrichtung, die die aufzubringende Kraft zum Bewegen von Lasten verringert und besteht aus einem Fixpunkt, aus festen Rollen, aus losen Rollen und aus einem Seil.
Wer den ersten Flaschenzug erfunden hat, ist nicht bekannt, aber dem griechischen Gelehrten Archimedes wird der zusammengesetzte Flaschenzug zugeschrieben, welcher tatsächlich bis in das 19. Jahrhundert hinein vom Prinzip her kaum abgeändert verwendet wurde.
Wie funktioniert ein Flaschenzug?
Wir haben ja schon folgende Bestandteile kennengelernt: Ein Fixpunkt, mindestens eine lose Rolle und eine feste Rolle und ein Seil.
Im besten Falle aber gibt es mehrere Rollen, denn, soweit können wir das Prinzip schon verraten, wird die aufzuwendende Kraft verringert, je mehr Rollen verwendet werden bzw. je mehr tragende Seilabschnitte dadurch entstehen.
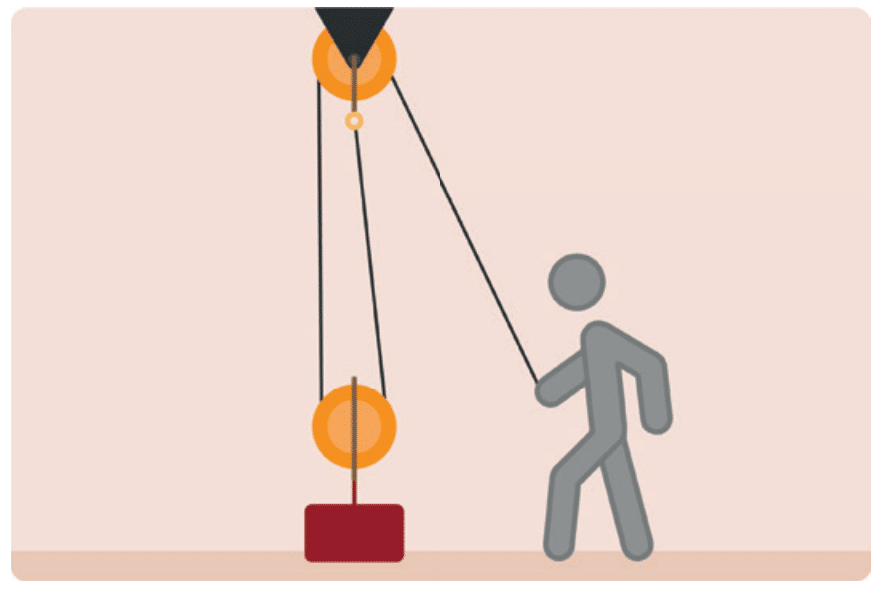
Stellen wir uns nun eine Last von 100 kg vor, welche durch unseren Flaschenzug gehoben werden soll.
An einem festen Punkt, z.B. an einem Dachbalken oder einem Kran, ist das Seil oben an dem Fixpunkt angebracht und darunter die sogenannte Umlenkrolle.
An der Last selbst von 100 kg ist eine sogenannte lose Rolle angebracht.
Und wenn wir nun das Seil, welches am Fixpunkt hängt, unten um eine lose Rolle und dann wieder oben um eine Umlenkrolle legen, so muss die Person, welche am Seil zieht, nur noch die halbe Kraft aufwenden, als ohne die Mechanik des Flaschenzuges.
Warum ist das so? Das erklären wir dir nun…
Mit welchen Formeln ist der Flaschenzug zu erklären?
Du hast nun das Grundprinzip vom Flaschenzug erfahren, doch gehen wir jetzt mal ins Detail.
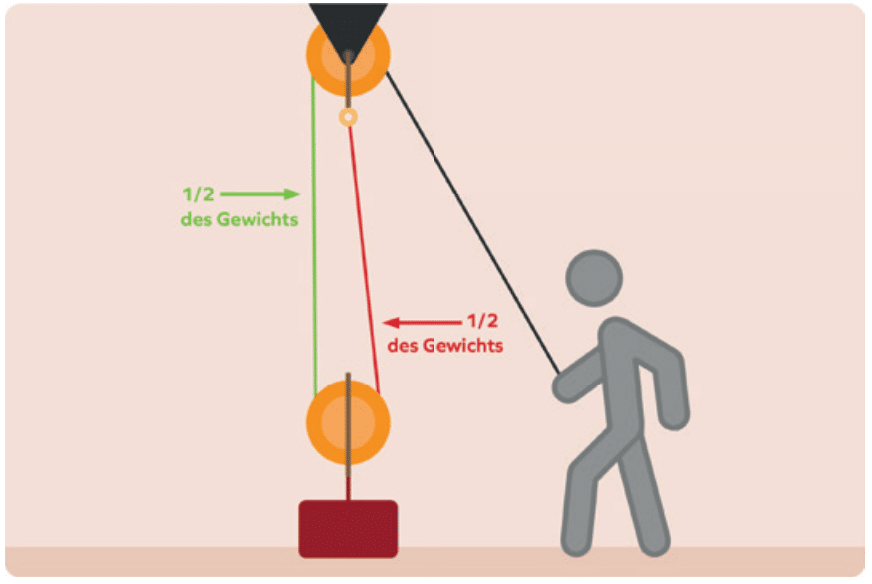
Hast du bei einer Last von 100 kg jeweils eine Umlenkrolle und eine lose Rolle, so verteilen sich ja die 100 kg auf zwei Seilstränge und dadurch halbiert sich die Kraft, die aufzuwenden ist zum Heben der Last auf 50 kg bzw. 500 Newton.
Erhöhst du nun die Anzahl an Rollen um eine weitere, so drittelst du sogar die aufzuwendende Kraft auf 333 N, da nun die Last auf drei tragende Seile verteilt wird.
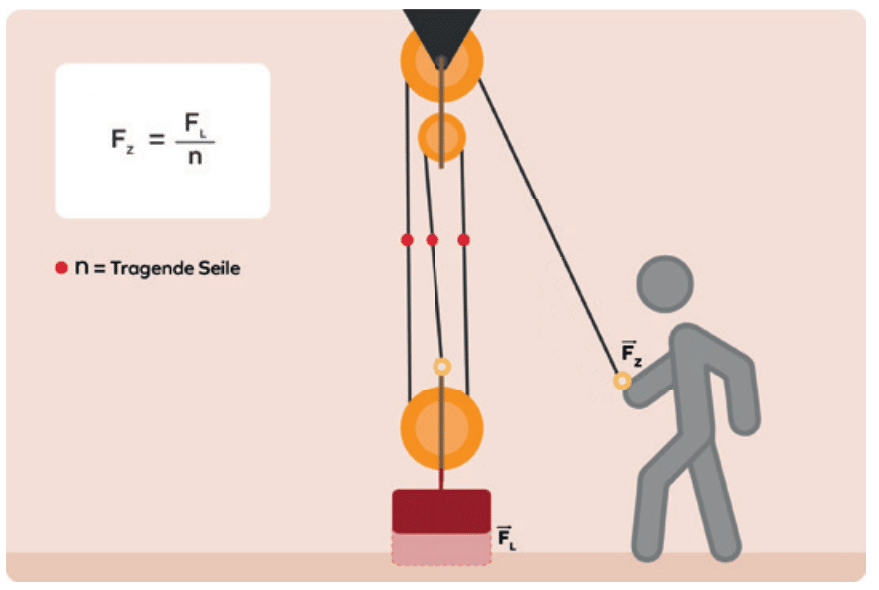
Und dieses Prinzip ist an sich unendlich fortzuführen und lässt sich mit einem Satz definieren:
Je größer die Zahl der tragenden Seile n ist, desto weniger Zugkraft FZ musst du aufbringen, um eine Last FL anzuheben.
Die Formel lautet also: FZ = FL / n
Und was ist mit dem Seil?
Während du das Prinzip der Rollen, ob Umlenkrolle oder lose Rolle, nun kennengelernt hast, so gibt es noch ein weiteres Prinzip zu beachten: je mehr Rollen du verwendest, umso mehr Seillänge musst du bewegen, also ziehen, um die Last entsprechend zu heben.
Doch diese Rechnung ist tatsächlich einfach, da sie den gleichen Faktor bedient.
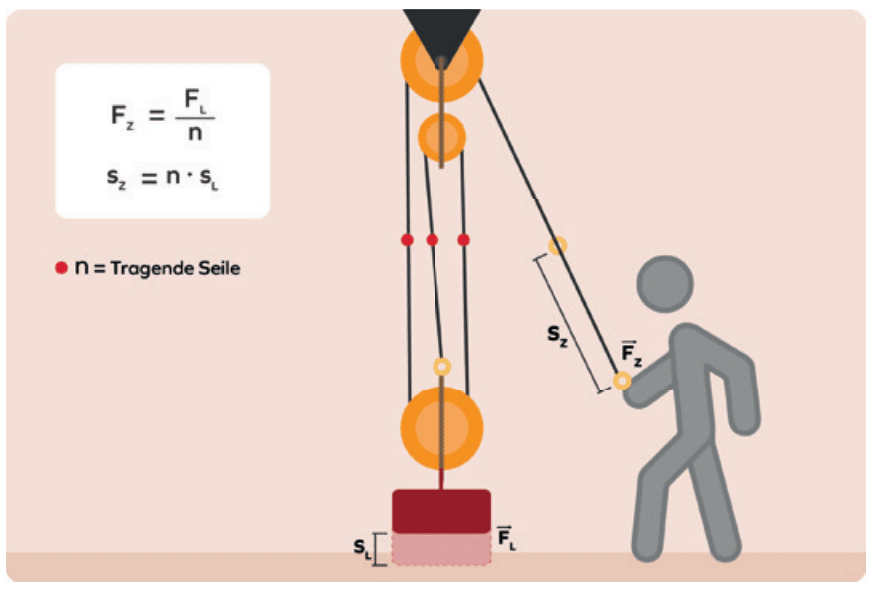
Bei der 100 kg Kiste und drei Rollen hat sich die aufzuwendende Kraft gedrittelt.
Willst du diese Kiste einen Meter durch den Flaschenzug anheben, so musst du nun für diesen einen Meter das dreifache an Seillänge ziehen, also: drei Meter!
Die notwendige Zugstrecke sZ erhöht sich also, je mehr tragende Seile n verwendet werden, um eine Last die Strecke sL anzuheben.
Hier lautet die Formel nun: sZ = n * sL
Beispielaufgabe 1
Lass uns nun einige Beispielaufgaben anschauen.
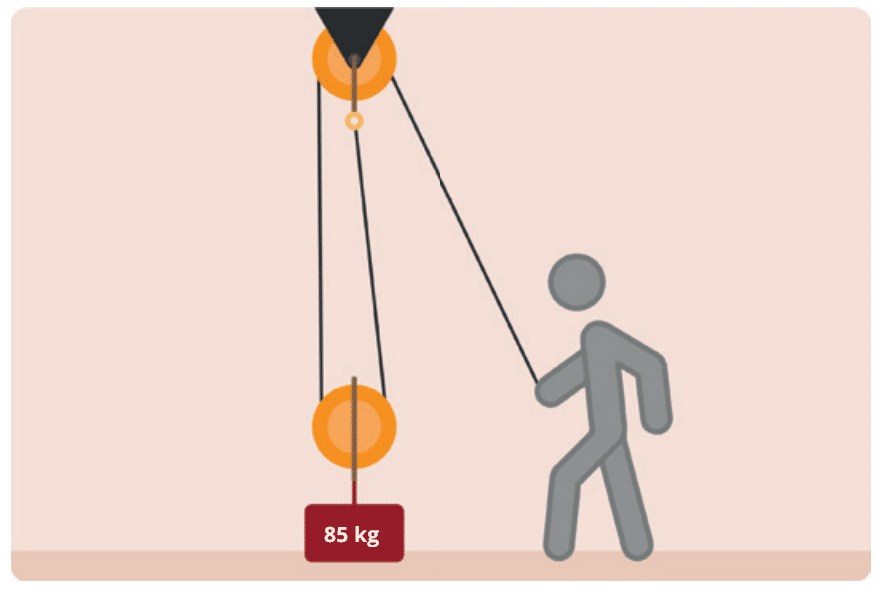
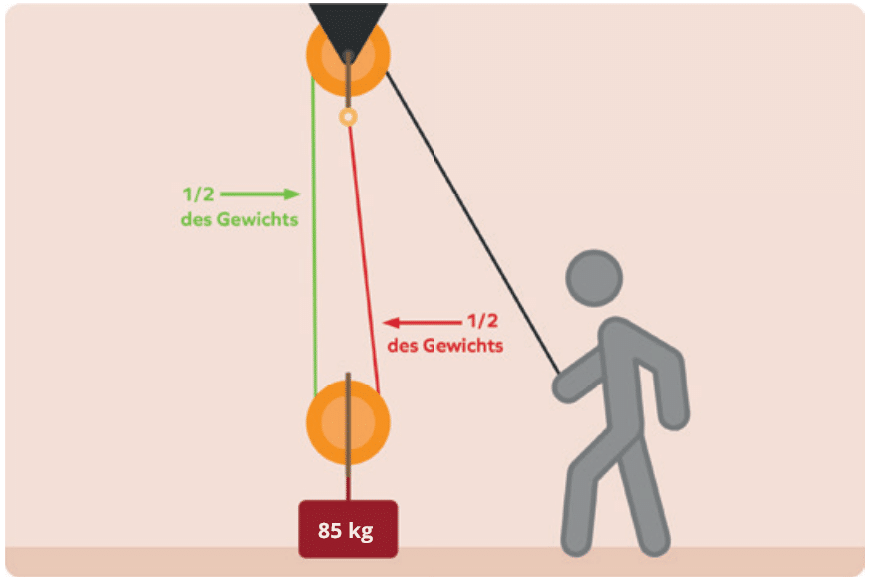
Hier in diesem Beispiel haben wir eine Last von 85 kg auf dem Boden liegen. Um diese anzuheben, wie groß ist die benötigte Kraft F in Newton?
- 405 N
- 420 N
- 425 N
- 525 N
Die korrekte Antwort lautet: 425 N, da zwei tragende Seile die aufzuwendende Kraft halbieren.
Beispielaufgabe 2
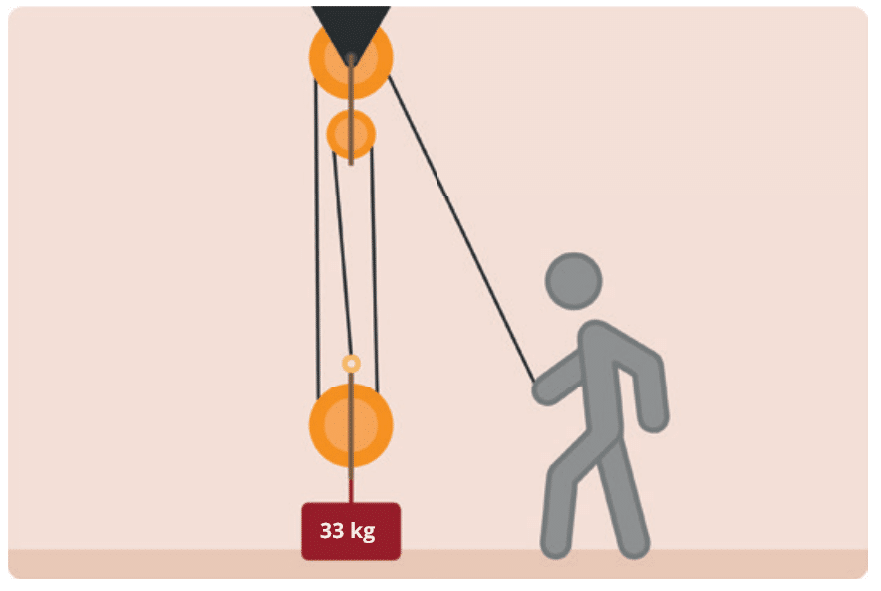
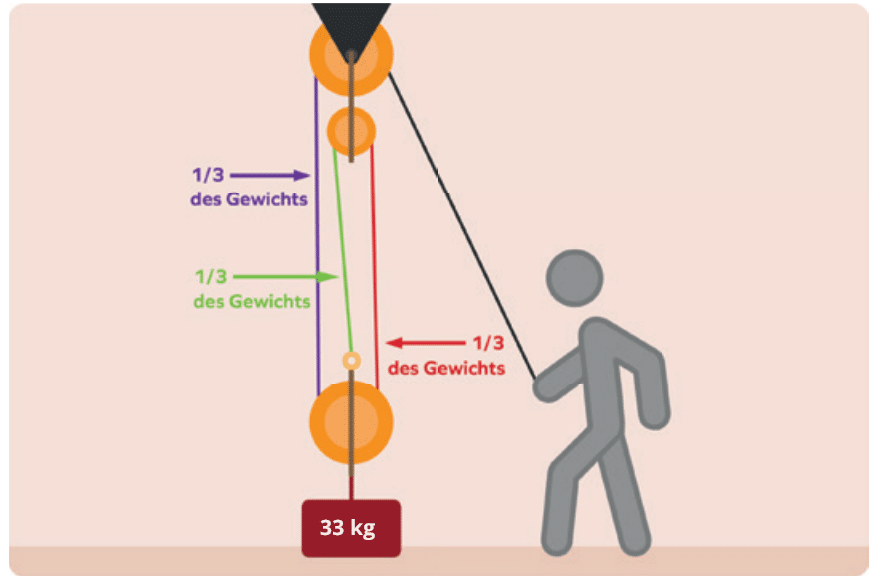
Bei unserem nächsten Beispiel möchten wir wissen, wie groß die benötigte Kraft F in Newton ist, wenn das Gewicht 33 kg beträgt?
- 115 N
- 120 N
- 110 N
- 100 N
Hier in diesem Beispiel lautet die korrekte Antwort 110 N.
Hast du es gewusst?
Genau, hier ist es ein Drittel im Verhältnis zur Last von 33 kg, da drei tragende Seile verwendet wurden.
Beispielaufgabe 3
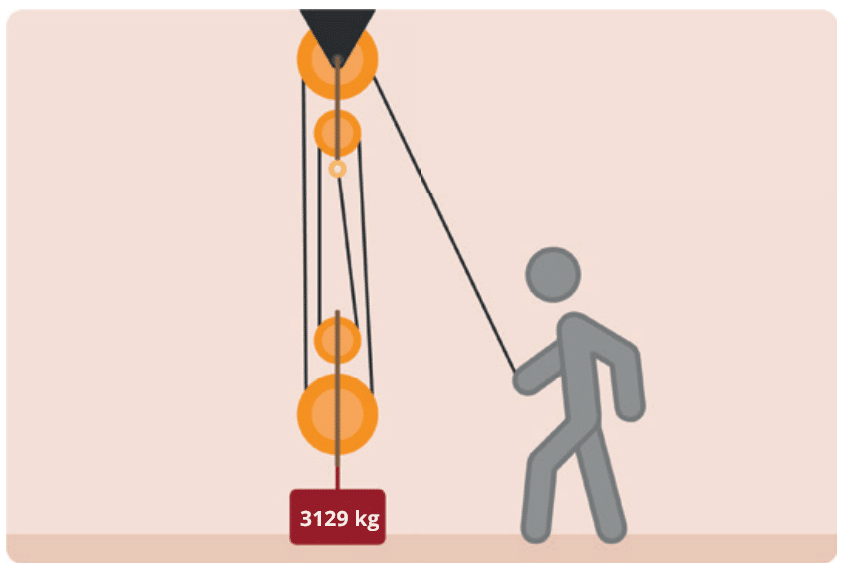
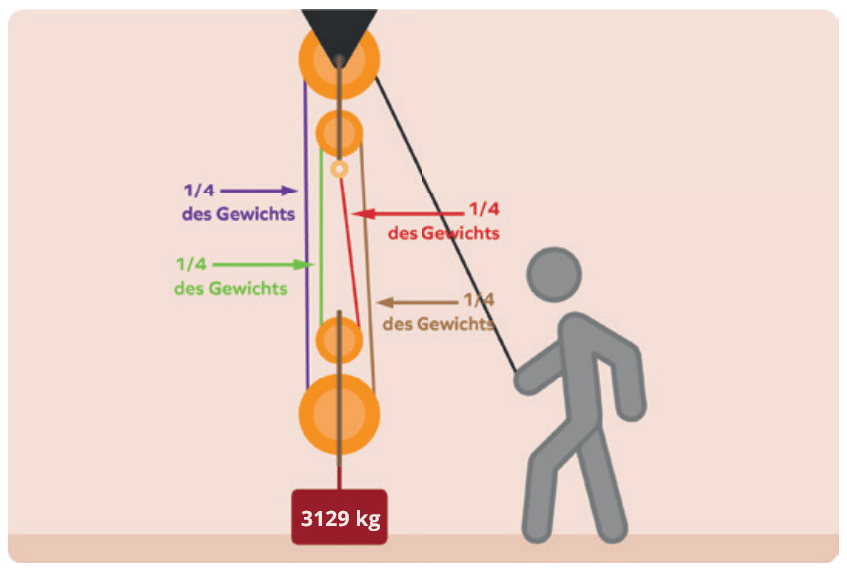
Kommen wir zu einer dritten Beispielaufgabe. Wie groß ist die benötigte Kraft F in kg, wenn das Gewicht 3.129 kg beträgt?
- 728,25 kg
- 782,25 kg
- 782,2 kg
- 782 kg
Hier lautet die Antwort 782,25 N.
Weißt du, warum das so ist?
Genau, hier sind vier tragende Seile zum Heben verwendet worden und somit wurde die notwendige Kraft geviertelt.
Beispielaufgabe 4
Lass uns noch eine letzte Beispielaufgabe durchgehen.
Erinnerst du dich noch an das Prinzip, dass sich die zu ziehende Seillänge vergrößert, je nachdem, wie viele Rollen bzw. tragende Seile verwendet werden, um die Last entsprechend anzuheben?
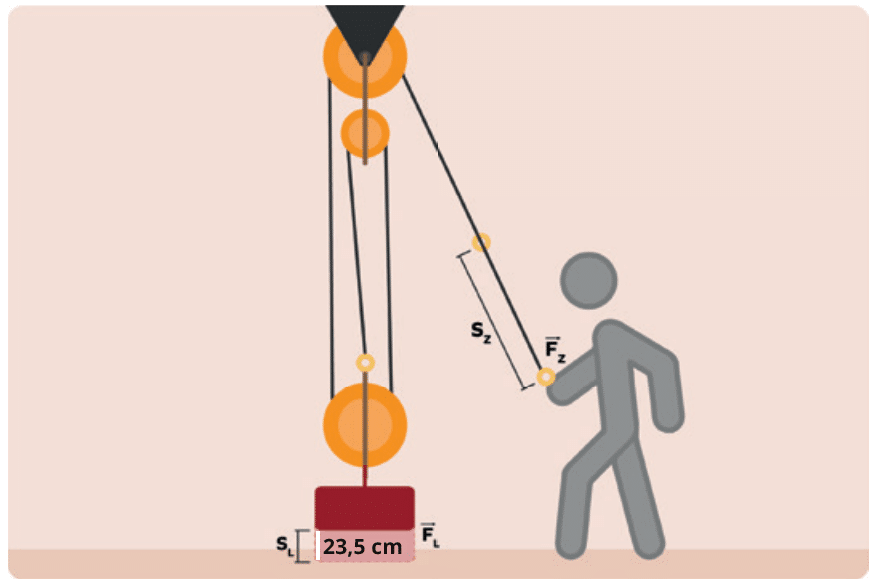
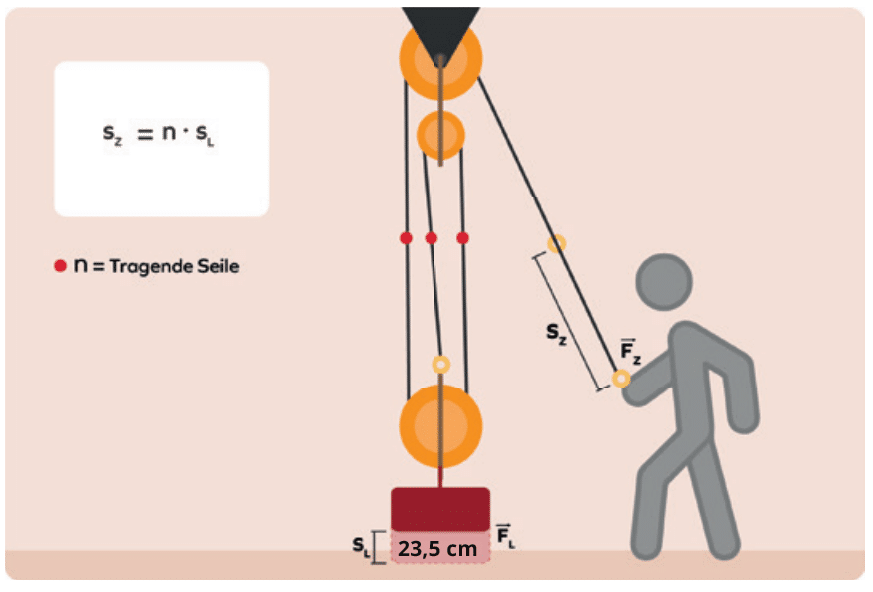
So fragen wir hier in der vierten Beispielaufgabe mal nicht nach der benötigten Kraft F, sondern nach der notwendigen Zugstrecke.
Wie lang ist also die Zugstrecke sZ in diesem Beispiel, wenn die Strecke der Last sL 23,5 cm beträgt?
- 70,25 cm
- 70,5 cm
- 71,5 cm
- 70 cm
Und, bist du auch auf das Ergebnis 70,5 cm gekommen?
Wenn ja, dann hast du das Prinzip des Flaschenzugs schon gut verstanden.
Wenn nicht, dann probiere es gerne weiter mit praktischen Aufgabenstellungen und deren Lösungen in der Plakos Akademie!
Übung Flaschenzug trainieren
Ein passender Online-Trainer, der dir zahlreiche Übungsaufgaben inkl. Lösungshinweisen zu verschiedenen Aufgabentypen bietet und deine Mathekenntnisse auffrischt, ist der Mathe Online Testtrainer von Plakos.
Hier findest du viele Lern- und Prüfungsinhalte zu mathematischen Grundlagen, zur numerischen Logik, zu Symbolen & Figuren oder zur Merkfähigkeit. Außerdem erhältst du zusätzlich die passende Lern-App, das heißt für dich: flexibel Lernen, wann und wo Du möchtest! Schaue dir also unbedingt den Mathe Online Testtrainer von Plakos an, um bei zukünftigen Tests besser abzuschneiden.
Dies war nun ein Einblick in mögliche Aufgaben zum Flaschenzug, die dich in einem Logik-Teil eines Einstellungstests erwarten können.
Wir wünschen Dir viel Spaß beim Üben und viel Erfolg bei Deinem Einstellungstest.
Dein Plakos Team