Wir erklären dir das Thema “Prozentrechnen im Einstellungstest” anhand von praktischen Beispielen und du kannst sofort mit Übungsaufgaben dein Wissen testen.
Aufgaben zum Prozentrechnen sind nicht nur in Matheklausuren an der Uni oder in der Schule ständig präsent, sondern werden gerade in Bewerbungsgesprächen immer beliebter, da Prozentrechnen eine Basis-Qualifikation darstellt, die in an sich allen Berufen sowie im persönlichen Alltag benötigt wird.
Zur optimalen Vorbereitung findest Du hier die Übungsaufgaben, welche leicht beginnen (Level 1) und steigern sich dann bis zum Level 5 und alle Aufgaben können im Kopf gerechnet werden. Du findest zudem hier auch einen weiteren Eignungstest sowie Einstellungstest.
Grundwissen zu Prozent
Prozent ist eine Hilfsmaßeinheit, welche meist kleinere Zahlen ins Verhältnis zu einem Hundertstel setzt. Prozentangaben werden durch das Symbol % (ausgesprochen Prozent) kenntlich gemacht.
% ist also das gleiche wie 1/100
Beispiel 1: 45 % kann als Bruch 45/100 oder als Dezimalzahl 0,45 geschrieben werden.
Beispiel 2: Der Bruch ½ ist das gleiche wie 0,5 als Dezimalzahl oder 50 %.
Beispiel 3: 0,125 ist das gleiche wie 12,5 % oder 125/1000 bzw. 1/8 als Bruch. Jede Zahl lässt sich in eine Prozentzahl umrechnen und jede Prozentzahl lässt sich in eine Dezimalzahl umrechnen.
Beispiel 4: 1 % als Dezimalzahl -> 1 % ist das gleiche wie 1 mal 1/100 also 0,01 als Dezimalzahl.
Beispiel 5: Zahlen in % -> Um auf die Prozentzahl zu kommen wird die Zahl mal 100 % genommen, also z.B. 5 
Beispiel 6: Brüche in Prozent -> Nun wird die Bruchzahl mal 100 % genommen, also z.B. 4/5 
Prozentrechnungsaufgaben mit einer Formel lösen
In vielen Prozentrechenaufgaben sind zwei Angaben vorhanden und es soll ein dritter Wert ermittelt werden. Dabei dreht es sich immer um drei Werte:
Grundwert (G): Der Grundwert ist eine beliebige Zahl, die für 100 % steht.
Beispiel: Der Bauer hat insgesamt 90 Apfelbäume. (90 Apfelbäume entspricht hier 100 %, also dem Grundwert)
Prozentwert (W): Der Prozentwert ist die wertmäßige Angabe bezogen auf den Grundwert.
Beispiel: Der Bauer hat insgesamt 90 Apfelbäume und will 18 weitere anpflanzen. (18 steht hier für den Prozentwert)
Prozentsatz (p): Der Prozentsatz gibt das Verhältnis vom Prozentwert zum Grundwert in % wieder.
Beispiel: Der Bauer hat insgesamt 90 Apfelbäume und will 18 weitere anpflanzen. Das sind 20 %. (20 % steht für den Prozentsatz).
Die Formel lautet grundsätzlich -> p = W : G · 100 %
Bezogen auf unser Beispiel lautet die Formel: p = 18 (Prozentwert / weitere Apfelbäume) : 90 (Grundwert / vorhandene Apfelbäume) · 100 % = 20 %
Die Aufgabe lässt sich natürlich auch anders herum stellen, sodass der der Prozentsatz 18 bereits gegeben ist, und der Prozentwert (W) gesucht ist: W = G : 100 · p
Beispiel: W = 90 : 100 · 20 = 18
Genauso kann in der Aufgabe nur der Prozentwert und Prozentsatz gegeben sein und der Grundwert (G) wird gesucht: G = W : p · 100
Beispiel: G = 18 : 20 · 100 = 90
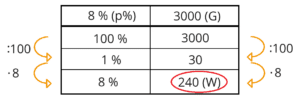
Prozentrechnen mit dem Dreisatz
Der Dreisatz eignet sich sehr gut, wenn eine Aufgabe im Kopf gerechnet werden soll. Zum Dreisatz gibt es ein eigenes Kapitel unter Dreisatz im Einstellungstest und Übungsaufgaben.
Weitere Fragen zum Thema “Prozentrechnen im Einstellungstest”?
Dies war ein erster Einblick zum Thema Prozentrechnen im Einstellungstest.
Gerne kannst du uns auch in die Kommentare schreiben, wenn du dir nicht sicher bist und weitere Fragen hast!
Herzliche Grüße und viel Erfolg gewünscht!
Dein Team von Plakos!













2 Antworten
eine aktie ist von 6,60€ auf 7,37€ gestiegen also 77cent um wieviel prozent ist die aktie gestiegen
bitte rechen beispiel ohne die protzenttaste auf der tastatur.danke.
gegeben: Grundwert G = 6.6 € Prozentwert W = 0.77 €
gesucht: Prozentsatz p (die 0.77 € als Prozentangabe)
Formel: W / G * 100 = p
Rechnung: 0.77€ / 6.6 € * 100 = 11.67 % (gerundet auf 2. Stelle nach Komma)