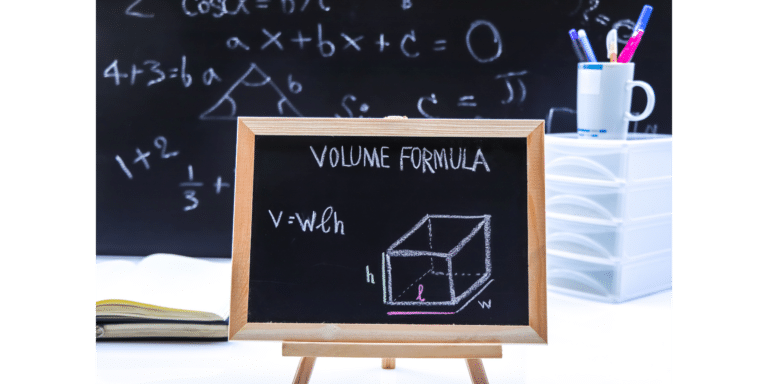Körperberechnung / Volumenberechnung – Aufgaben

Körperberechnung wird im Mathematikunterricht in den höheren Klassen behandelt. Die Aufgaben aus der Geometrie zur Bestimmung des Körpervolumens lassen sich durch passende Formeln relativ leicht lösen. Häufig fangen wir bei den Übungsaufgaben zunächst mit einfacheren Körpern wie Würfel, Quader, Zylinder, Pyramide, Kegel oder Kugel an. Die nächste Stufe sind dann häufig zusammengesetzte Figuren, die zur Bestimmung des Volumens zunächst in einzelne Körperformen aufgeteilt werden müssen.

Formeln zur Volumenberechnung

Bei der Ermittlung des Volumens ist es meist hilfreich zunächst die Fläche einer Ansicht zu bestimmen. Das sollte man vorher natürlich mit unseren Aufgaben zur Flächenberechnung üben. Sobald man die Fläche berechnet hat, muss nur noch eine Dimension hinzugefügt werden, um das dreidimensionale Volumen des Körpers zu bestimmen.

	Körperberechnung Würfel Ein Würfel hat die Eigenschaft, dass alle 12 Kanten gleich lang sind. Außerdem sind alle Winkel rechtwinklig = 90°. Somit gehört die Formel zur Körperberechnung des Würfels zu den Einfacheren.Formel Würfel-Volumen: V = a³
	Körperberechnung Quader Der Quader besteht aus sechs rechteckigen Flächen, dessen Winkel alle rechtwinklig sind. Der Quader hat außerdem insgesamt 12 Kanten, von denen jeweils vier Kanten gleich lang und parallel zueinander sind.Formel Quader-Volumen: V = a · b · c
	Körperberechnung Zylinder Ein Zylinder hat eine Grund-, und Deckfläche die parallel und deckungsgleich zueinander verlaufen. Außerdem besitzt der Zylinder eine Mantelfläche, die aus parallelen Geraden gebildet wird. In der Umgangssprache ist mit einem Zylinder immer ein Kreiszylinder gemeint, welcher durch Verschiebung eines Kreises parallel zu einer Geraden durch den Kreismittelpunkt entsteht.Formel Zylinder-Volumen: V = r² · π · h
	Körperberechnung Prismen Ein Prisma bzw. Mehrzahl-Prismen sind geometrische Körper mit einem Vieleck als Grundfläche. Oftmals werden Prismen mit einem Dreieck als Grundfläche in den Beispielen verwendet. Prismen entstehen durch eine Parallelverschiebung der Grundfläche entlang einer Geraden. Ist die Verschiebung senkrecht zur Grundfläche, handelt es sich um einen geraden Prisma, ansonsten ist es ein schiefer Prismakörper.Formel Prismen-Volumen: V = Ag · h
	Körperberechnung Pyramide Die Pyramide hat immer ein Vieleck als Grundfläche, welches durch Dreiecke umschlossen wird. Die Dreiecke treffen sich an der Spitze der Pyramide auf einem Punkt. Die Dreiecke bilden somit die Mantelfläche der Pyramide. Je nachdem welche Figur die Pyramide als Grundfläche hat, spricht man u.a. von einer quadratischen, rechteckigen, fünfseitigen oder sechsseitigen Pyramide.Formel Pyramide-Volumen: V = (a² · h) x 1/3
	Körperberechnung Kegel Der Kegel hat immer eine runde Grundfläche, welche mit einem Punkt außerhalb der Grundfläche verbunden ist. Diesen Punkt nennt man den Scheitelpunkt. Der Mantel umschließt den Scheitelpunkt und die runde Grundfläche. Der Abstand zwischen dem Scheitelpunkt und der Grundfläche ist die Höhe des Kegels. Beim geraden Kegel liegt der Scheitelpunkt immer genau über dem Mittelpunkt der Grundfläche.Formel Kegel-Volumen: V = (r² · π · h)/3
	Körperberechnung Kugel Eine Kugel entsteht durch die Drehung einer Kreislinie um einen Kreisdurchmesser, man nennt diese Fläche auch Rotationsfläche. Zieht man durch die Kugel einen Schnitt, so entsteht immer eine Kreisfläche.Formel Kugel-Volumen: V = (4 · r³ · π)/3

Noch mehr Matheaufgaben mit Online Lösungen oder zum Ausdrucken gibt es u.a. auf unseren Seiten Flächenberechnung, Mathetest, Grundrechenarten und Geometrie.

Körperberechnung im Mathematikunterricht: Verstehen, Anwenden, Lösen

Die Körperberechnung gehört zu den wichtigsten Themen im Bereich der Geometrie und wird in der Regel in den höheren Klassenstufen ab der 7. oder 8. Klasse eingeführt – je nach Bundesland und Schulform. Dabei geht es im Kern darum, das Volumen von dreidimensionalen geometrischen Körpern zu berechnen. Anders als bei der Flächenberechnung, bei der nur die Ausdehnung in zwei Dimensionen (Länge und Breite) betrachtet wird, kommt bei der Volumenberechnung die dritte Dimension – die Höhe bzw. Tiefe – hinzu.

Die Körperberechnung hilft, reale Objekte mathematisch zu erfassen. Egal ob man sich ein Schwimmbecken, eine Getränkedose, eine Pyramide in Ägypten oder einen Wassertank vorstellt – hinter all diesen Dingen stecken geometrische Grundformen, deren Volumen sich mit Hilfe mathematischer Formeln berechnen lässt. Dabei beginnt der Unterricht in der Regel mit einfachen Körpern wie Würfeln oder Quadern und steigert sich dann zu komplizierteren Formen wie Zylindern, Pyramiden oder zusammengesetzten Körpern.

Ein solides Verständnis der Körperberechnung ist nicht nur im Mathematikunterricht, sondern auch in vielen Berufen und im Alltag von Bedeutung. Technische Berufe wie Bauzeichner, Ingenieure, Architekten oder Mechatroniker arbeiten regelmäßig mit Volumenangaben – sei es bei der Konstruktion von Bauteilen, der Berechnung von Materialmengen oder der Planung von Räumen. Auch in handwerklichen Berufen wie dem Tischlerhandwerk oder in der Logistik (z. B. beim Beladen eines Containers) spielt das Volumen eine zentrale Rolle.

Von der Fläche zum Volumen

Der Einstieg in die Körperberechnung erfolgt oft über einen konzeptionellen Brückenschlag: Zunächst wird wiederholt, wie man die Fläche einer geometrischen Figur berechnet – etwa Rechteck, Dreieck oder Kreis. Anschließend wird dieses Flächenwissen genutzt, um das Volumen zu berechnen. Die Grundidee dabei ist einfach: Volumen = Grundfläche × Höhe. So ergibt sich beispielsweise das Volumen eines Quaders aus der Fläche des Rechtecks (Grundfläche) multipliziert mit der Höhe. Diese Vorstellung erleichtert das Verständnis und schafft eine Verbindung zwischen zweidimensionalen und dreidimensionalen Objekten.

Körperformen und ihre Eigenschaften

Würfel und Quader sind ideale Einsteigerformen. Sie bestehen ausschließlich aus rechteckigen Flächen und besitzen ausschließlich rechte Winkel. Ihre Kanten sind leicht zu erfassen und zu benennen, die Formeln zur Volumenberechnung sehr übersichtlich. Beim Würfel, bei dem alle Kanten gleich lang sind, lautet die Formel einfach: V = a³. Beim Quader, der aus drei verschiedenen Kantenlängen besteht, lautet sie: V = a × b × c.

Zylinder und Kegel stellen bereits eine Steigerung dar, da sie runde Grundflächen besitzen. Hier wird das Formelwissen zur Kreisfläche gebraucht, denn bei beiden Formen bildet ein Kreis die Basis. Das Volumen des Zylinders berechnet sich mit: V = π × r² × h. Der Kegel hat die gleiche Formel, allerdings wird das Ergebnis noch durch 3 geteilt: V = (π × r² × h) / 3. Diese Gemeinsamkeit macht es Schüler:innen oft leichter, sich beide Formeln gleichzeitig zu merken.

Pyramiden und Prismen sind besonders interessante Körper, da sie im Alltag selten in Reinform vorkommen, in der Mathematik aber wichtige Prinzipien veranschaulichen. Bei der Pyramide ist das Volumen ein Drittel der Grundfläche multipliziert mit der Höhe, also V = (A × h) / 3. Prismen dagegen sind besonders wichtig, wenn zusammengesetzte Körper betrachtet werden – sie bestehen in vielen Fällen aus mehr als nur einer regelmäßigen Grundfläche.

Kugeln sind eine besondere Form, da sie weder Kanten noch Ecken besitzen und sich in keine typische Fläche oder Linie einordnen lassen. Ihre Volumenformel lautet: V = (4/3) × π × r³ – sie zeigt, dass bei der Berechnung von Kugeln ausschließlich der Radius notwendig ist.

Zusammengesetzte Körper – der nächste Schwierigkeitsgrad

Hat man die Grundformen verstanden, geht es im Unterricht oft weiter mit zusammengesetzten Körpern. Diese bestehen aus zwei oder mehr Grundformen, die zusammengefügt wurden – zum Beispiel ein Zylinder auf einem Quader oder eine Pyramide auf einem Prisma. In solchen Fällen ist es wichtig, den Körper in seine Einzelteile zu zerlegen, die Volumen jeweils einzeln zu berechnen und anschließend wieder zusammenzuführen. Diese Art der Aufgabenstellung erfordert räumliches Denken, strategisches Vorgehen und gutes Formelverständnis.

Es ist dabei besonders hilfreich, sich die Körper nicht nur abstrakt vorzustellen, sondern sie sich auch aufzuzeichnen – mit allen Maßen und Flächenbezeichnungen. Wer einmal verstanden hat, dass eine große Wasserflasche ein Zylinder mit Deckel und Boden ist oder ein Zelt als Pyramide dargestellt werden kann, dem fällt das Anwenden des Gelernten deutlich leichter.

Häufige Fehlerquellen und wie man sie vermeidet

Trotz klarer Formeln und vieler Hilfestellungen unterlaufen beim Rechnen mit Körpern häufig Fehler. Dazu zählen:

• Verwechselung von Radius und Durchmesser: Gerade beim Zylinder oder der Kugel wird oft der Durchmesser eingesetzt, obwohl die Formel mit dem Radius arbeitet.

• Fehler bei der Flächenberechnung der Grundfläche: Wenn diese falsch berechnet wird, ist automatisch das Volumen falsch.

• Unvollständige Maßeinheiten: Wird beispielsweise die Grundfläche in cm² berechnet und die Höhe in m eingesetzt, stimmt das Ergebnis nicht – auch wenn die Rechenmethode korrekt ist.

• Fehler beim Umrechnen von Längeneinheiten oder Volumen (z. B. cm³ in Liter).

• Rechenfehler bei Brüchen, insbesondere bei Pyramide und Kegel, bei denen ein Drittel der Grundfläche multipliziert wird.

Um diese Fehler zu vermeiden, sollte man sich Rechenschritte systematisch aufschreiben und vor dem Einsetzen der Werte immer prüfen, ob alle Maßeinheiten zueinander passen.

Bedeutung für weiterführende Themen

Die Körperberechnung ist nicht nur ein isoliertes Thema, sondern Grundlage für viele weitere mathematische und physikalische Themen. In der Physik ist das Volumen unerlässlich, um Dichte, Auftrieb, Masse oder Druck zu berechnen. Auch in der Chemie spielt das Volumen z. B. bei Stoffmengenkonzentrationen eine Rolle. In der höheren Mathematik bilden Volumenberechnungen die Grundlage für Integralrechnung, Rotationskörper, Rauminhalte von Funktionen oder Volumenvergleiche zwischen verschiedenen Körpern.

Fazit: Körperberechnung als Schlüssel zum Raumverständnis

Die Körperberechnung ist weit mehr als das Auswendiglernen von Formeln. Sie hilft uns, Raum zu begreifen, mathematisch zu durchdringen und praktisch zu nutzen. Wer sich mit Würfeln, Quadern, Pyramiden und Zylindern beschäftigt, erkennt die Ordnung hinter der Welt der Formen – und schafft damit eine Grundlage für viele Berufe und Lebensbereiche.

Regelmäßiges Üben, sorgfältiges Arbeiten und das Verständnis der zugrunde liegenden Flächenberechnungen sind dabei die entscheidenden Erfolgsfaktoren. Mit wachsender Erfahrung wird das Rechnen mit Körpern immer einfacher – und vielleicht sogar zu einem echten Aha-Erlebnis: Denn wer Volumen berechnet, rechnet nicht nur – sondern denkt in Dimensionen.