Allgemeines über Matrizen
Der Begriff “Matrizen” steht für die Mehrzahl von Matrix, welcher im Jahre 1850 zuerst in die Logik eingeführt wurde. Diese Elemente können nun Zahlen, Buchstaben oder Figuren sein, welche gegenseitige Zusammenhänge darstellen sollen, ob über Spalten, Zeilen oder Diagonalen.
Das Ergebnis dieser Ansammlung an Elementen ist ein rechteckiges Schema, welches eben Matrix heißt.
Die allgemeine Form einer Matrix besteht aus m Zeilen und n Spalten und die Position der Elemente wird mit einem Doppelindex (11, 12, 1n, etc.) gekennzeichnet. Dabei gibt der erste Index die Zeile und der zweite Index die Spalte an.
Oftmals findest sich daher genau diese Darstellung zum besseren Verständnis:
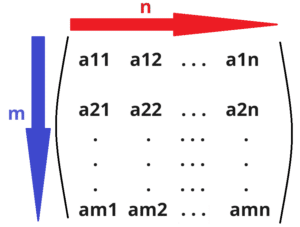
Entsprechend dieser Anzahlen ist die Ordnung der Matrix definiert: Die obige Ideal-Matrix ist eine (m x n)-Matrix.
Wenn du z.B. folgende Matrix vorfindest…

… so ist dies eine (4 x 3)-Matrix.
Du siehst, dies ist letztlich gar nicht kompliziert.
Eine sehr ähnliche Form findet man in den Buchstabenmatrizen, in denen Buchstabenreihen fortgesetzt werden, wobei i.d.R. jeder Buchstabe für eine Zahl im Alphabet steht.
Addition & Subtraktion und Multiplikation
Nun lassen sich auch verschiedene Zahlenmatrizen z.B. addieren, multiplizieren usw. und da es um die tabellarische Anordnung von Zahlen geht, so lassen sich lineare Gleichungssysteme gut beschreiben und einfach lösen.
Addition von Matrizen
Bei der Addition von Matrizen werden die einzelnen Komponenten der Matrizen jeweils addiert.
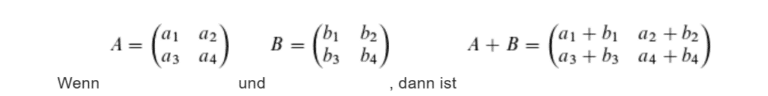
Subtraktion von Matrizen
Bei der Subtraktion von Matrizen werden die einzelnen Komponenten der Matrizen jeweils subtrahiert.
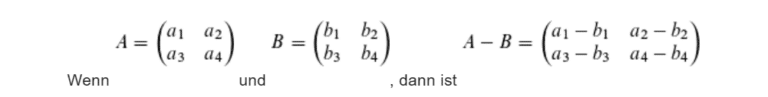
Multiplikation einer Matrix mit einem Skalar
Wenn man eine Matrix mit einem Skalar multiplizieren möchte, so wird der Skalar mit jeder Komponente der Matrix einzeln multipliziert.

Multiplikation von zwei Matrizen
Bei der Multiplikation von zwei Matrizen AxB berechnet man das Skalarprodukt von der jeweiligen Zeile der Matrix A und der Spalte der Matrix B.
Achtung! Zwei Matrizen A und B können nur miteinander multipliziert werden, wenn die Spaltenanzahl der Matrix A mit der Zeilenanzahl der Matrix B übereinstimmt.

FAQ Matrizentest im Einstellungstest
Ein Matrizentest ist eine Form des Intelligenztests, bei dem Bewerber Muster und logische Zusammenhänge zwischen verschiedenen geometrischen Figuren oder Symbolen erkennen müssen. Matrizentests sind besonders in Auswahlverfahren für Berufe wie Polizei, Bundeswehr oder Unternehmen beliebt, weil sie unabhängig von sprachlichen oder kulturellen Kenntnissen sind und die kognitiven Fähigkeiten der Bewerber direkt messen.
Der Aufbau eines typischen Matrizentests sieht folgendermaßen aus:
Matrix-Struktur: Die Matrix besteht aus mehreren Reihen und Spalten, die jeweils ein Muster oder eine regelmäßige Veränderung in den dargestellten Symbolen zeigen.
Mustererkennung: Die Testperson muss ein regelmäßiges Muster in der Anordnung der Symbole erkennen, wie zum Beispiel eine Veränderung in Form, Größe, Anzahl oder Ausrichtung der Symbole.
Fehlendes Element: In vielen Fällen fehlt in der Matrix ein Element, das von den Bewerbern korrekt identifiziert werden muss. Die Aufgabe besteht darin, das richtige Symbol oder die richtige Figur auszuwählen, die das Muster vervollständigt.
Steigende Schwierigkeit: Die Aufgaben werden oft zunehmend schwieriger, wobei die Muster komplexer und abstrakter werden, um die kognitiven Fähigkeiten und das logische Denken der Person zu testen.
Matrizentests sind besonders geeignet, um die kognitiven Fähigkeiten zu messen, da sie keine sprachlichen oder kulturellen Kenntnisse erfordern und das abstrakte Denken und die logische Problemlösungsfähigkeit betonen.
Der Matrizentest misst die kognitiven Fähigkeiten, insbesondere abstraktes Denken, Mustererkennung und Problemlösungsfähigkeiten. Er ist sprachneutral und zeigt, wie gut jemand Zusammenhänge erkennt und logische Schlüsse zieht. Personen, die gut abschneiden, weisen häufig eine hohe kognitive Flexibilität und Verarbeitungsgeschwindigkeit auf, was für viele berufliche und soziale Situationen wichtig ist.
Der Matrizentest ist besonders geeignet, um die intellektuelle Leistungsfähigkeit ohne Beeinflussung durch kulturelle oder sprachliche Unterschiede zu bewerten. Er wird daher häufig in Auswahlverfahren verwendet, um die Problemlösungsfähigkeiten und das logische Denkvermögen von Bewerbern zu testen, unabhängig von ihrem Bildungshintergrund. Ein gutes Abschneiden im Matrizentest kann auf eine hohe intellektuelle Flexibilität und die Fähigkeit hinweisen, auch in komplexen und sich schnell ändernden Situationen effizient zu denken und zu handeln.
Die Dauer eines Matrizentests variiert je nach Testformat und Anzahl der Aufgaben, liegt jedoch normalerweise zwischen 20 und 45 Minuten. In vielen Fällen besteht der Test aus 20 bis 30 Aufgaben, die innerhalb eines festgelegten Zeitrahmens gelöst werden müssen. Die Dauer kann auch von der Schwierigkeit des Tests und den spezifischen Anforderungen des Auswahlverfahrens abhängen.
Um sich auf einen Matrizentest vorzubereiten, sollten Sie regelmäßig Übungstests machen, die sich auf Mustererkennung und logisches Denken konzentrieren. Es ist hilfreich, verschiedene Arten von Musteraufgaben zu üben, um ein besseres Verständnis für die verschiedenen Arten von Mustern und deren Variationen zu entwickeln. Zudem können Puzzles, Sudoku oder rätselhafte Logikaufgaben das analytische Denken stärken.
Durch regelmäßiges Üben verbessern Sie nicht nur Ihre Reaktionsgeschwindigkeit, sondern auch Ihre Fähigkeit, Zusammenhänge schnell zu erkennen und abstrakt zu denken.
Unser Online Testtrainer führt dich durch die verschiedenen Disziplinen in den Matrizentest und bereitet dich optimal anhand interaktiver Übungen und Lernvideos vor.
In diesem Video siehst du viele Infos zum Thema „Matrizentests im Einstellungstest“ aus einem unserer wöchentlichen Webinare. Klicke HIER für zahlreiche weitere Clips im Plakos YouTube Channel!
Wichtige Tipps und Techniken zur Lösung
Matrizentest-Aufgaben lassen sich mit Hinblick auf einen bevorstehenden Einstellungstest, IQ-Test oder Eignungstest üben. Da die Aufgaben in solchen Tests sich immer wieder ähneln, kann eine Vorbereitung sehr hilfreich sein.
Ein Matrizentest prüft das logische und strukturierte Denken, die (räumliche) Vorstellungskraft und die Fähigkeit aus komplexen Sachverhalten heraus die richtigen Schlussfolgerungen ziehen zu können. Diese Art von Tests liegt nicht von Grund auf jedem, umso wichtiger sind Übungen, um ein bestimmtes Muster in der Aufgabenstellung schnell erkennen zu können.
Vergleiche die Figuren in einer Reihe, Zeile, Diagonale und auch im sich überlappenden Gesamtbild. Wie ähnelt sich die erste Figur der zweiten, die zweite der dritten, usw. Ist eine bestimmte Tendenz zu erkennen?
Wenn es dir bei der Suche nach Gemeinsamkeiten schwer fällt eine Tendenz zu erkennen, so achte auch auf Unterschiedlichkeiten. Möglicherweise fügst du dir auf diesem Weg das eine oder andere weiteres Puzzlestück hinzu, um ein Muster zu erkennen.
Die einzelnen Elemente können sich in verschiedensten Möglichkeiten ähneln oder unterscheiden, achte hier auf Anzahl, Position, Farbe, Größe, Art und auch Richtung der Elemente.
Der Matrizentest lässt sich gut trainieren
Ganz egal, ob man sich im Eignungstest für ein Studium, einem Einstellungstest für einen Ausbildungsplatz, in einem Assessment Center oder einem anderen Auswahlverfahren befindet: Eine gute Vorbereitung ist das A und O und wir empfehlen dir dazu unseren Online Testtrainer „Matrizentest im Einstellungstest 2024“.
Herzliche Grüße und viel Erfolg gewünscht!
Dein Team von Plakos!
Beispielaufgaben aus dem Kurs
- Aufgabe 01
- Lösung 01
Erkennst du eine Regelmäßigkeit bei den Positionen der Kreise?
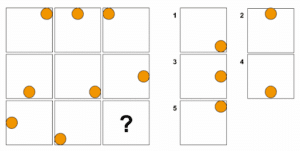
Antwort 4, da jede Zeile waagerecht zu betrachten ist. Die Kreise bewegen sich dabei gegen den Uhrzeigersinn eine Position weiter.
- Aufgabe 02
- Lösung 02
Achte auf identische Muster / Formen und deren Verteilung.
Antwort 2, da das mittlere Kästchen einer Reihe jeweils umgeben ist von identischen Figuren.
- Aufgabe 03
- Lösung 03
Es gilt auch Kombinationen von Formen, Farben und Richtungen zu beachten.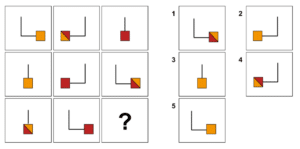
Antwort 2, da das mittlere Kästchen einer Reihe jeweils umgeben ist von identischen Figuren.
- Aufgabe 04
- Lösung 04
Diese Aufgabe prüft die Subtraktionsregel. Die Elemente im dritten Feld (C) ergeben sich aus der Differenz zwischen Feld 1 (A) und Feld 2 (B): A – B = C.
Die Figur ergibt sich aus der Subtraktion von Feld 1 und Feld 2.


